D4 The Hardy-Weinberg Principle

Previous
Next


D.4.1  Explain how the Hardy-Weinberg equation is derived

The Hardy-Weinberg equation predicts the frequency of two alternate alleles in a population

It is used for traits that show classical Mendelian inheritance:

  • Only two alleles for a gene (one dominant and one recessive allele)
  • Follows autosomal inheritance (not sex-linked traits)


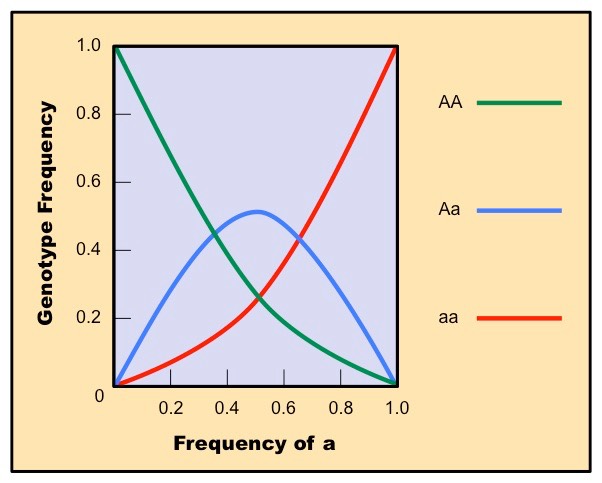
For two alleles of a given genetic characteristic, three genotypes will exist:  AA, Aa and aa

  • Dominant allele is A, with a frequency of p
  • Recessive allele is a, with a frequency of q


The total frequency of both alleles will be 1 (i.e. p + q = 1)

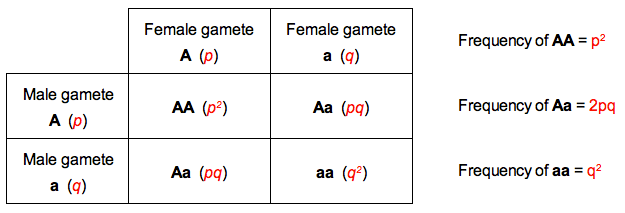
  • Because genotype frequencies consist of two alleles, the equation must be squared: (p + q)2 = 1


This gives the expanded form of the Hardy-Weinberg equation: p2 + 2pq + q2 = 1


Deriving the Hardy-Weinberg Equation

Screen Shot 2013-01-30 at 3.43.10 PM


D.4.2  Calculate allele, genotype and phenotype frequencies for two alleles of a gene, using the Hardy-Weinberg equation

Suppose we had a population of 500 individuals, in which 9% of individuals were albino (albinism is a recessive characteristic ð aa)

Using the equations:   p + q = 1   and   p2 + 2pq + q2 =1

•  If q2 = 0.09   ð   q = 0.3  (√0.9)

•  If q = 0.3   ð   p = 0.7  (p + 0.3 = 1)

•  If p = 0.7   ð   p2 = 0.49  (0.7 × 0.7)

•  Therefore 2pq = 0.42  (2 × 0.7 × 0.3)


Substituting these numbers for frequencies and applying them to our original population, we find that:

  • 49% are homozygous dominant (AA), which is 245 individuals  (0.49 × 500)
  • 42% are heterozygous (Aa), which is 210 individuals  (0.42 × 500)
  • 9% are homozygous recessive (aa), which is 45 individuals  (0.09 × 500)


Representative Population ð Albinism Frequency = 9%

albinism genetics


D.4.3  State the assumptions made when the Hardy-Weinberg equation is used

  • When the Hardy-Weinberg equation is used in population genetics, it is assumed that a constant allele frequency will be maintained over time
  • For this to occur it is implied that:
    • The population is large
    • There is random mating
    • There is no mutation
    • There is no gene flow (immigration or emigration)
    • There is no natural selection or allele-specific mortality


Graphical Representation of the Hardy-Weinberg Equation

hardy-weinberg