Populations are fluid and are subject to continual change in numbers through natality, mortality and migration

• Populations may be large and impractical to count unless the species is large and the target area is small

Population sampling involves identifying individual numbers in small areas and then extrapolating to estimate population totals

• The difference between the estimate of population size and the true size of the whole population is known as the sampling error
  

• The more samples that are taken (and the larger the sampling area), the more accurate population estimates are likely to be
  

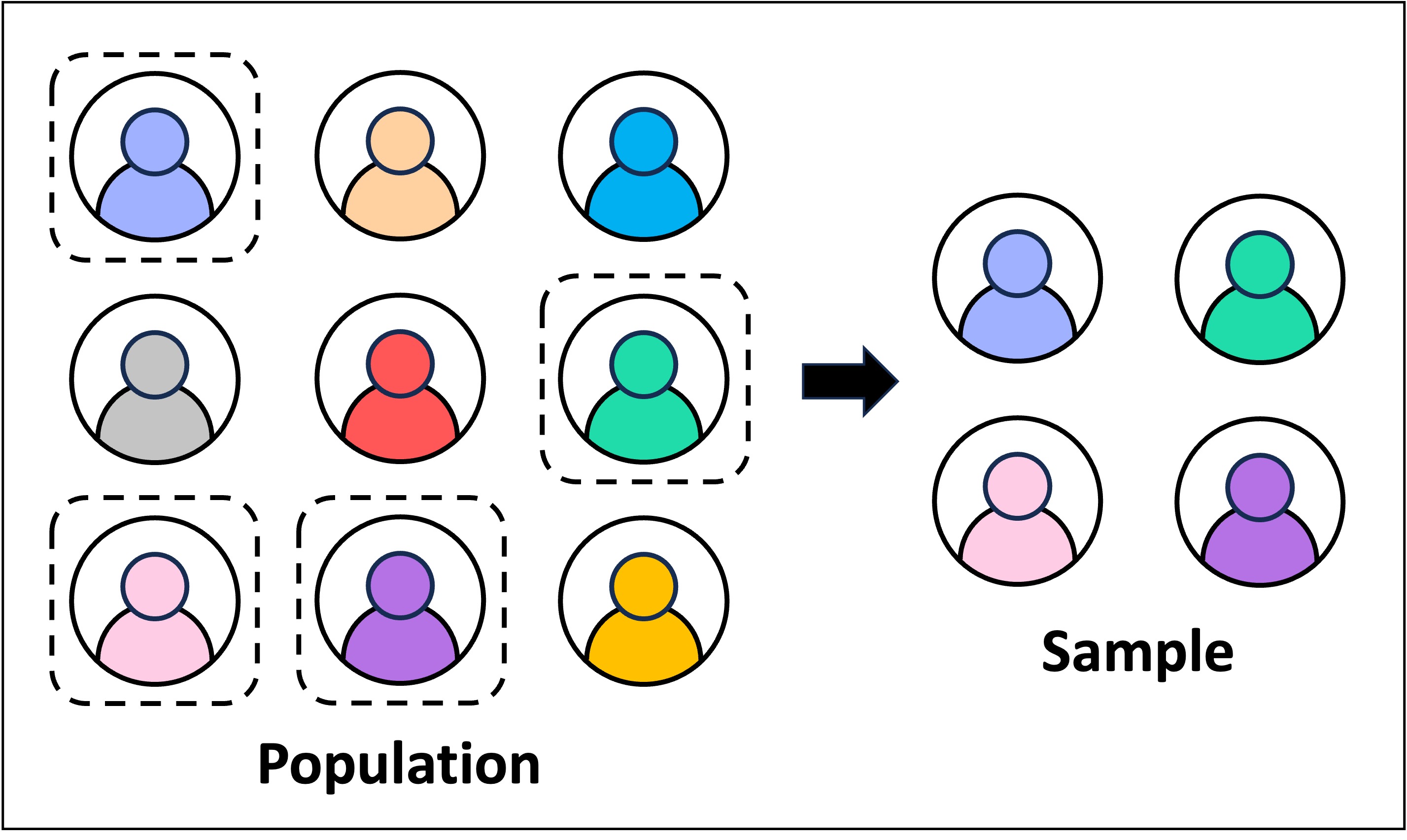
In random sampling, the positions of the sampling points are selected at random to avoid the potential for bias

• Sampling sites can be randomly selected by establishing a grid of the target area and arbitrarily assigning grid coordinates

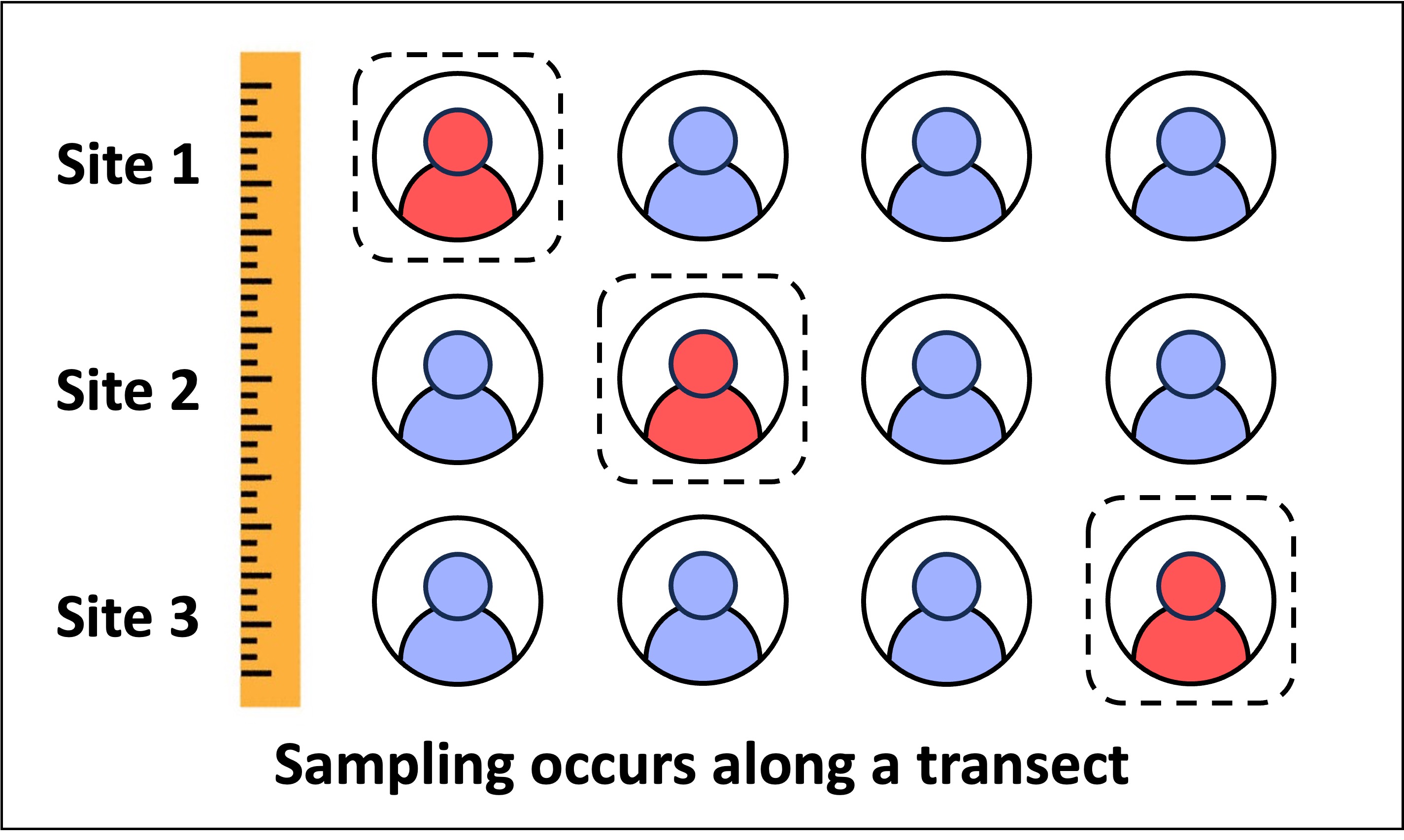
In systematic sampling, the positions of the sampling points are assigned at fixed intervals throughout the target area

• This allows for the investigation of the effect of a changing environmental factor on species distribution (via a transect)

Population Sampling

Quadrat Sampling

The population size or distribution of a non-motile (sessile) species can be determined using quadrat sampling 

• A quadrat is a rectangular frame of known dimensions that can be used to establish population densities
  

• Quadrats are placed inside a defined area in either a random arrangement or according to a transect
  

• The number of individuals of a given species is either counted or estimated via percentage coverage
  

If the sampling process is repeated many times, a mean and standard deviation can be calculated

• The standard deviation shows the degree of data spread and could be used to indicate how evenly distributed the population is across the habitat

Counting Sessile Species